| Rumus Bangun Datar | ||
|---|---|---|
 | ||
| Bangun Datar | Rumus | |
| Keliling | Luas | |
| Persegi Panjang | K = 2p + 2l | L = p x l |
| Persegi | K = 4 x s | L = s x s |
| Segitiga | K = a + b + c | L = 1/2 x a x t |
| Belah Ketupat | K = 4a | L = 1/2 x d1 x d2 |
| Lingkaran | K = 22/7 x d | L = 22/7 x r x r |
| Jajar Genjang | K = 2a + 2b | L = a x t |
| Trapesium | K = a + b + c + d | L = 1/2 x (a + b) x t |
| Layang-layang | K = a + b + c + d | L = 1/2 x d1 x d2 |
Rumus Bangun Datar atau Bidang Datar adalah Rumus Matematika dasar dari suatu area atau bentuk datar 2 dimensi yang dibatasi oleh garis-garis lurus atau lengkung. Area bidang datar ini terdiri dari beberapa bentuk termasuk: persegi, segitiga, jajaran genjang, persegi panjang, trapesium, layang-layang, belah ketupat, dan lingkaran. Secara singkat, area datar tersebut memiliki nilai kuantitas keliling dan luas dalam satuan panjang dan satuan luas.
Keliling dan Luas suatu bentuk bangun datar dapat diukur dengan menggunakan rumus. Nilai hasil dari ukuran tersebut dihitung berdasarkan standar satuan internasional, satuan keliling adalah meter (disingkat m), dan satuan luas adalah meter persegi (disingkat meter2). Kita juga bisa menghitungnya sesuai kebutuhan dengan satuan cm untuk keliling dan satuan cm2 untuk luas.
Rumus-rumus Keliling dan Luas Bangun Datar
Rumus Persegi Panjang
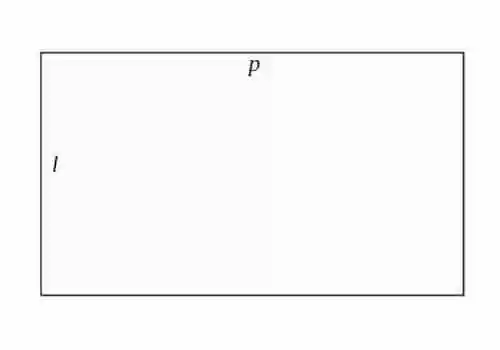
Persegi Panjang adalah bidang datar yang berbentuk segi empat dan terdiri dari 2 pasang sisi yang sejajar serta sama panjang dan keempat sudutnya mempunyai sudut siku-siku. Dibawah ini terdapat Rumus Keliling dan Luas Persegi Panjang.
Rumus Keliling Persegi Panjang
Rumus Keliling Persegi Panjang adalah K = 2p + 2l atau K = 2 x (p + l)
Keterangan Variabel:
K = Keliling
p = panjang
l = lebar
Rumus Luas Persegi Panjang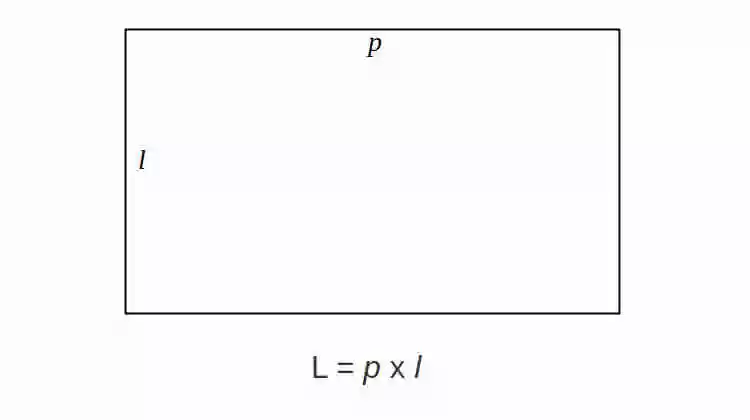
Rumus Luas Persegi Panjang adalah L = p x l
Keterangan Variabel:
L = Luas
p = panjang
l = lebar
Rumus Persegi (Bujur Sangkar)
Persegi atau Bujur Sangkar adalah bidang datar yang berbentuk segi empat dan terdiri dari 4 sisi yang sama panjang serta keempat sudutnya mempunyai sudut siku-siku. Dibawah ini terdapat Rumus Keliling dan Luas Persegi.
Rumus Keliling Persegi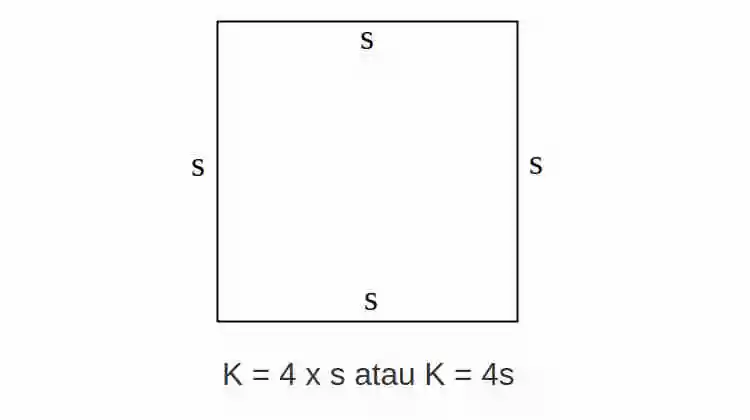
Rumus Keliling Persegi adalah K = 4 x s atau K = 4s
Keterangan Variabel:
K = Keliling
s = panjang atau lebar sisi
Rumus Luas Persegi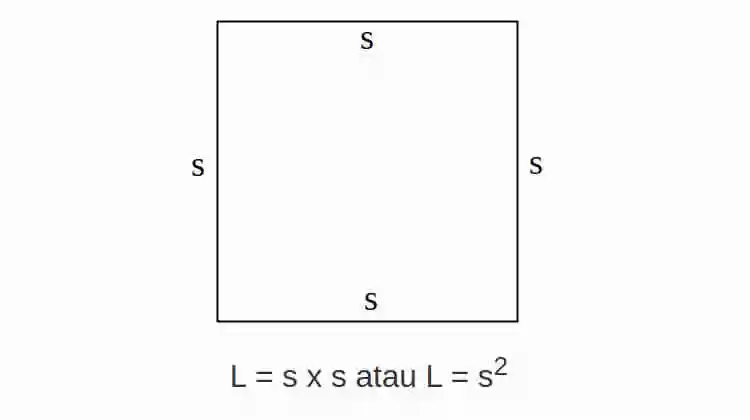
Rumus Luas Persegi adalah L = s x s atau L = s2
Keterangan Variabel:
L = Luas
s = panjang atau lebar sisi
Rumus Segitiga
Segitiga adalah bidang datar yang berbentuk dari 3 buah sisi dan mempunyai 3 buah sudut. Berdasarkan panjang, segitiga terdiri dari beberapa macam: segitiga sama sisi, segitiga sama kaki, segitiga sembarang. Berdasarkan besar sudut, segitiga terdiri dari: segitiga tumpul, segitiga siku-siku dan segitiga lancip. Dibawah ini terdapat Rumus Keliling dan Luas Segitiga.
Rumus Keliling Segitiga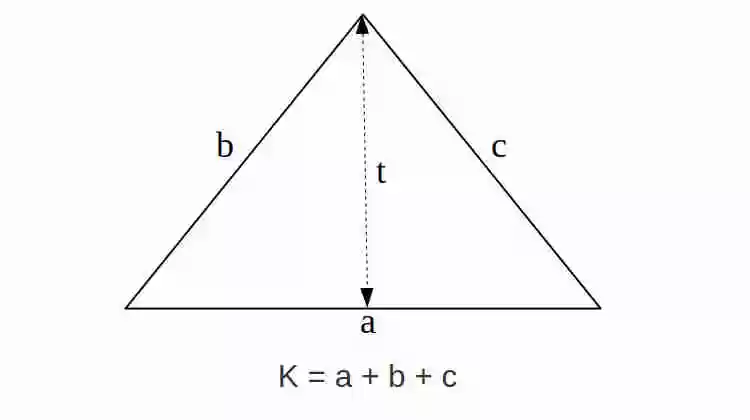
Rumus Keliling Segitiga adalah K = a + b + c
Keterangan Variabel:
K = Keliling
a, b, c = panjang masing-masing sisi
Rumus Luas Segitiga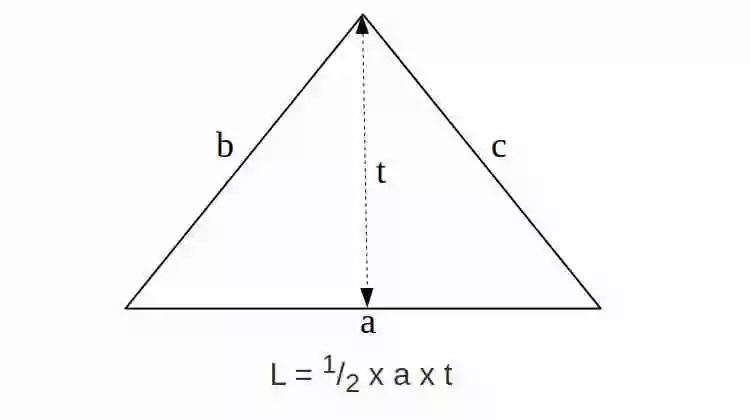
Rumus Luas Segitiga adalah L = 1/2 x a x t
Keterangan Variabel:
L = Luas
a = alas
t = tinggi
Rumus Belah Ketupat
Belah Ketupat adalah bidang datar yang berbentuk segi empat dan terdiri dari 4 sisi yang sama panjang serta kedua diagonalnya berpotongan tegak lurus. Dibawah ini terdapat Rumus Keliling dan Luas Belah Ketupat.
Rumus Keliling Belah Ketupat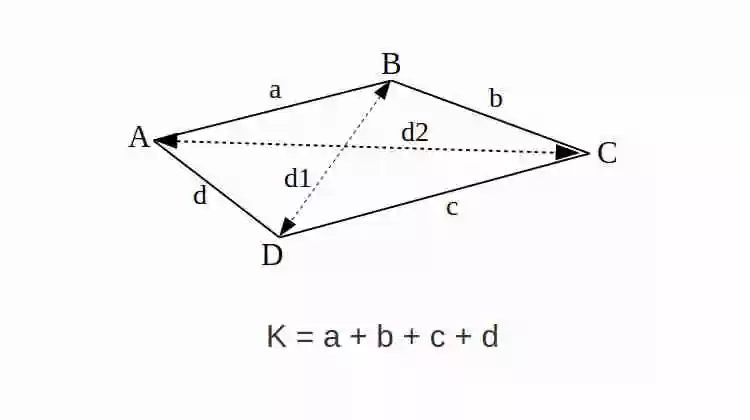
Rumus Keliling Belah Ketupat adalah K = a + b + c + d
Belah Ketupat biasanya memiliki 4 sisi yang sama, oleh karena itu a = b = c = d, sehingga Keliling bisa juga dihitung dengan Rumus K = 4a atau K = 4b atau K = 4c atau K = 4d.
Keterangan Variabel:
K = Keliling
a, b, c, d = panjang masing-masing sisi
Rumus Luas Belah Ketupat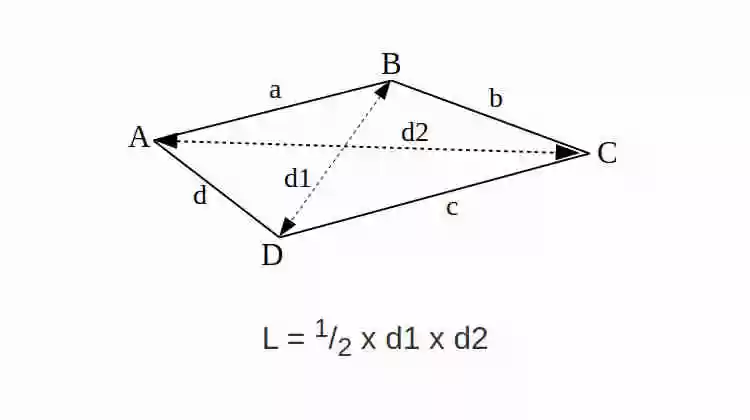
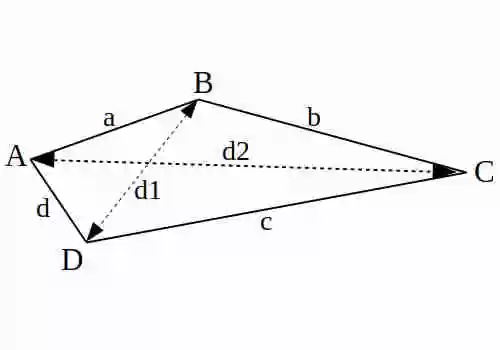
Rumus Luas Belah Ketupat adalah L = 1/2 x d1 x d2
Keterangan Variabel:
L = Luas
d1 = panjang diagonal 1 atau panjang dari B ke D
d2 = panjang diagonal 2 atau panjang dari A ke C
Rumus Lingkaran
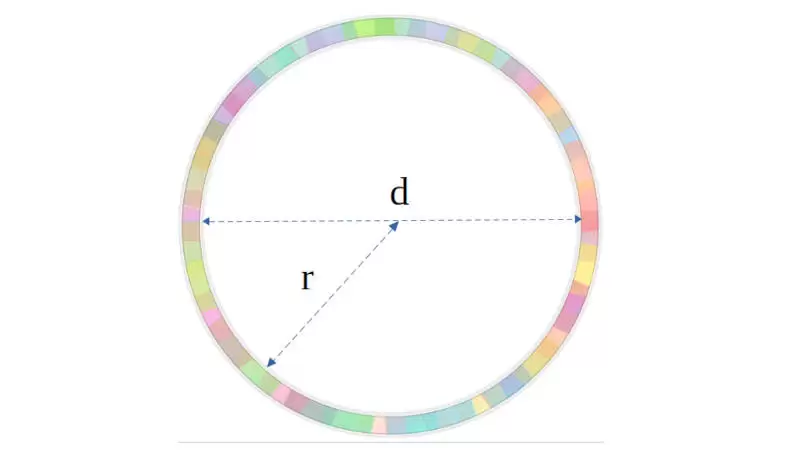
Lingkaran adalah bidang datar yang berbentuk dari himpunan semua titik persekitaran yang mengelilingi suatu titik pusat dengan jarak yang sama. jarak tersebut dikenal dengan nama jari-jari atau radius. Dibawah ini terdapat Rumus Keliling dan Luas Lingkaran.
Rumus Keliling Lingkaran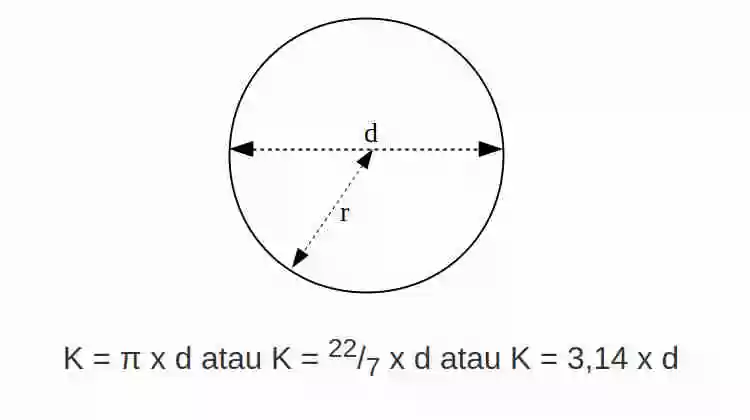
Rumus Keliling Lingkaran adalah K = π x d atau K = 22/7 x d atau K = 3,14 x d
Keterangan Variabel:
K = Keliling
π = phi, yaitu 22/7 atau 3,14 (nilai yang mendekati phi)
d = panjang diameter
Rumus Luas Lingkaran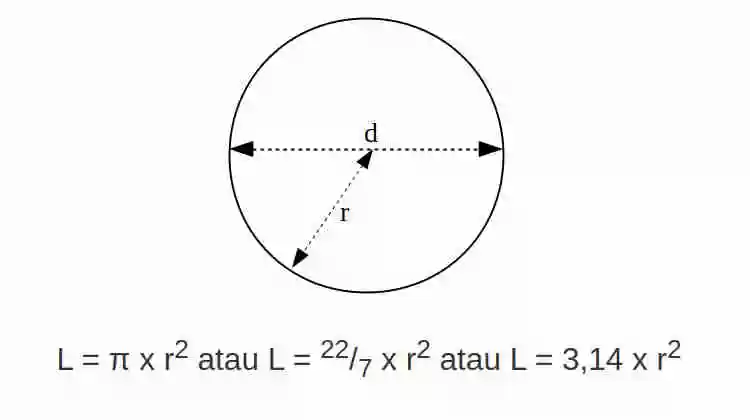
Rumus Luas Lingkaran adalah L = π x r2 atau L = π x r x r
Bisa juga dihitung dengan rumus:
L = 22/7 x r2 atau L = 22/7 x r x r
L = 3,14 x r2 atau L = 3,14 x r x r
Keterangan Variabel:
L = Luas
r = panjang jari-jari
π = phi, yaitu 22/7 atau 3,14 (nilai yang mendekati phi)
Rumus Jajar Genjang
Jajar Genjang adalah bidang datar yang berbentuk segi empat yang terdiri dari 2 pasang sisi yang sejajar, berhadapan dan sama panjang serta sudut-sudutnya yang berhadapan sama besarnya. Dibawah ini terdapat Rumus Keliling dan Luas Jajar Genjang.
Rumus Keliling Jajar Genjang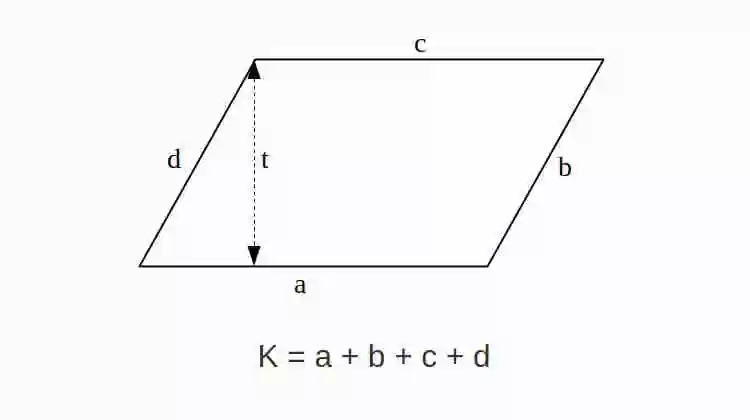
Rumus Keliling Jajar Genjang adalah K = a + b + c + d atau K = 2a + 2b
Keterangan Variabel:
K = Keliling
a, b, c, d = panjang masing-masing sisi
Rumus Luas Jajar Genjang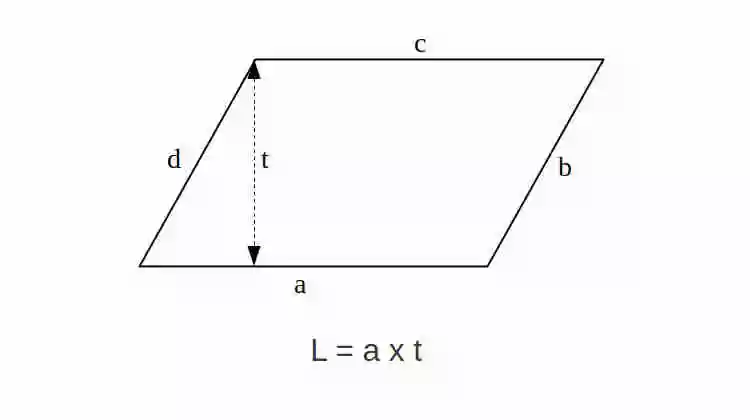
Rumus Luas Jajar Genjang adalah L = a x t
Keterangan Variabel:
L = Luas
a = alas
t = tinggi
Rumus Trapesium
Trapesium adalah bidang datar yang berbentuk segi empat dan mempunyai sepasang sisi yang sejajar serta sisi-sisi yang lain berbeda panjangnya. Dibawah ini terdapat Rumus Keliling dan Luas Trapesium.
Rumus Keliling Trapesium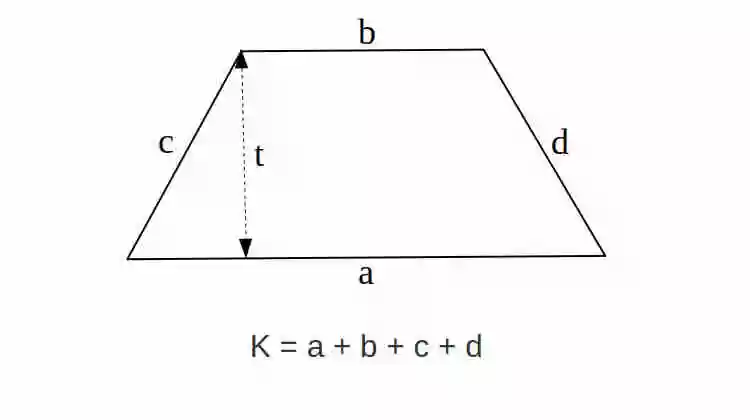
Rumus Keliling Trapesium adalah K = a + b + c + d
Keterangan Variabel:
K = Keliling
a, b, c, d = panjang masing-masing sisi
Rumus Luas Trapesium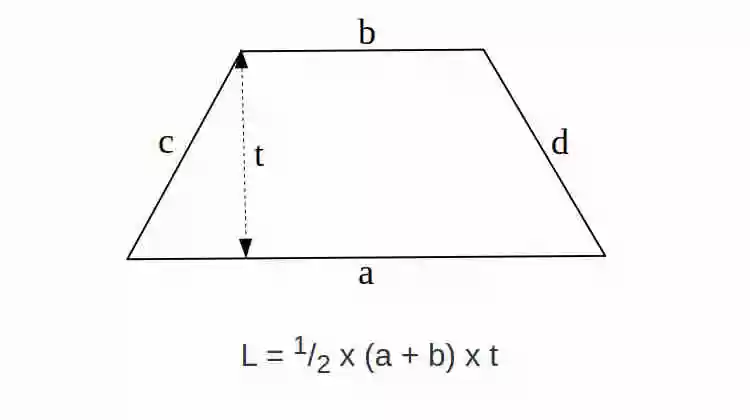
Rumus Luas Trapesium adalah L = 1/2 x (a + b) x t
Keterangan Variabel:
L = Luas
a = panjang sisi bawah
b = panjang sisi atas
t = tinggi
Rumus Layang-layang
Layang-layang adalah bidang datar yang berbentuk segi empat dan mempunyai 2 pasang sisi yang berdekatan sama panjang serta kedua diagonal berpotongan tegak lurus. Dibawah ini terdapat Rumus Keliling dan Luas Layang-layang.
Rumus Keliling Layang-layang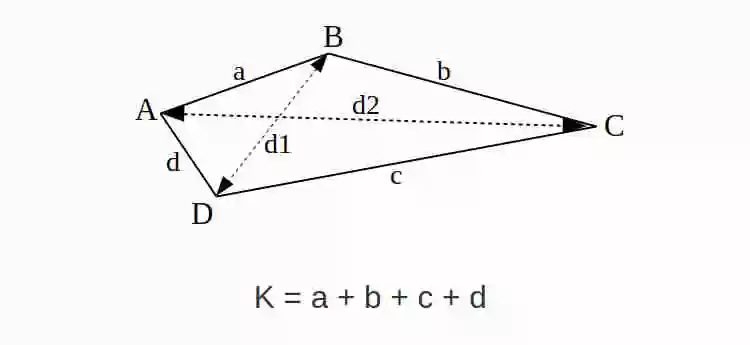
Rumus Keliling Layang-layang adalah K = a + b + c + d
Keterangan Variabel:
K = Keliling
a, b, c, d = panjang masing-masing sisi
Rumus Luas Layang-layang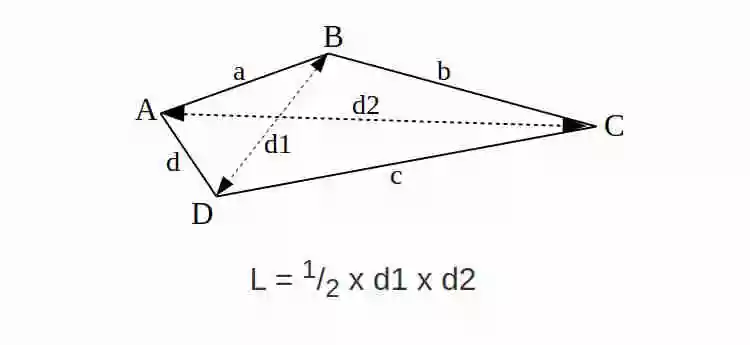
Rumus Luas Layang-layang adalah L = 1/2 x d1 x d2
Keterangan Variabel:
L = Luas
d1 = panjang diagonal 1 atau panjang dari B ke D
d2 = panjang diagonal 2 atau panjang dari A ke C
Rangkuman
Ada berbagai rumus-rumus perhitungan yang terkenal untuk bidang bentuk sederhana dalam matematika. Keliling dan Luas Area suatu bangun datar memainkan peran penting dalam matematika modern. Selain kepentingannya yang jelas dalam geometri dan perhitungan, luas terkait dengan definisi determinan dalam aljabar linier, dan merupakan properti dasar permukaan suatu bidang dalam variabel geometri.
Setiap hasil nilai satuan luas memiliki unit satuan yang sesuai. Dengan demikian, luas wilayah atau suatu area dapat diukur dalam meter persegi (m2), sentimeter persegi (cm2), milimeter persegi (mm2), kilometer persegi (km2), kaki persegi (ft2), yard persegi (yd2), mil persegi (mi2), dan sebagainya dan seterusnya. Secara aljabar, satuan ini dapat dianggap sebagai kuadrat dari satuan panjang yang sesuai. Satuan Internasional dari luas adalah meter persegi (m2).
Secara umum, luas bidang datar dalam matematika tingkat tinggi dipandang sebagai sesuatu yang khusus kuantitas untuk area dua dimensi. Area dapat diartikan melalui penggunaan aksioma, mendefinisikannya sebagai fungsi dari kumpulan bentuk bidang tertentu ke himpunan bilangan nyata atau aktual. Sehingga dapat dijelaskan bahwa fungsi seperti itu ada.