| Rumus Trapesium | ||
|---|---|---|
 | ||
| Bangun Datar | Rumus | |
| Keliling | Luas | |
| Trapesium | K = a + b + c + d | L = 1/2 x (a + b) x t |
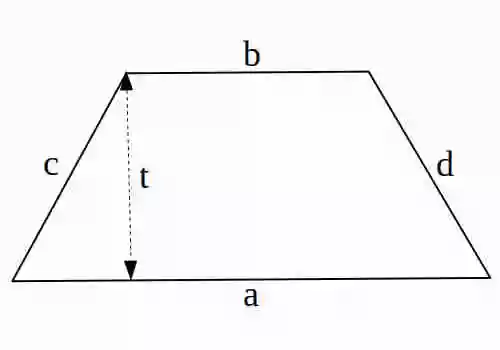
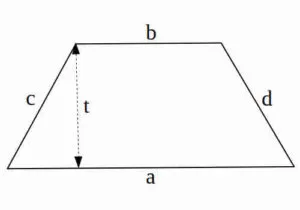
Rumus Trapesium adalah salah satu rumus bangun datar yang berbentuk segi empat dan mempunyai sepasang sisi yang sejajar serta sisi-sisi yang lain berbeda panjangnya. Keliling dan Luas Trapesium dapat diukur dengan menggunakan rumus.
Nilai hasil dari ukuran tersebut dihitung berdasarkan standar satuan internasional, satuan keliling adalah meter (disingkat m), dan satuan luas adalah meter persegi (disingkat m2). Kita juga bisa menghitungnya sesuai kebutuhan dengan satuan cm untuk keliling dan satuan cm2 untuk luas.
Rumus Keliling Trapesium
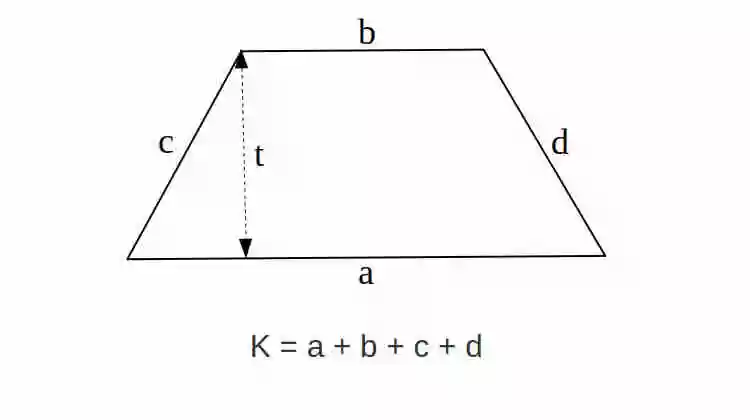
Rumus Keliling Trapesium adalah K = a + b + c + d
Keterangan Variabel:
K = Keliling
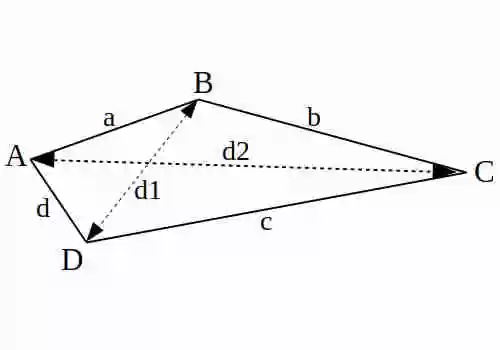
a, b, c, d = panjang masing-masing sisi
Contoh Soal: Suatu Trapesium memliki panjang a = 4 m (meter), b = 3 m (meter), c = 2 m (meter), d = 2 m (meter), berapakah keliling Trapesium?
Jawaban:
K = a + b + c + d
K = 4 m + 3 m + 2 m + 2 m
K = 11 m
Rumus Luas Trapesium
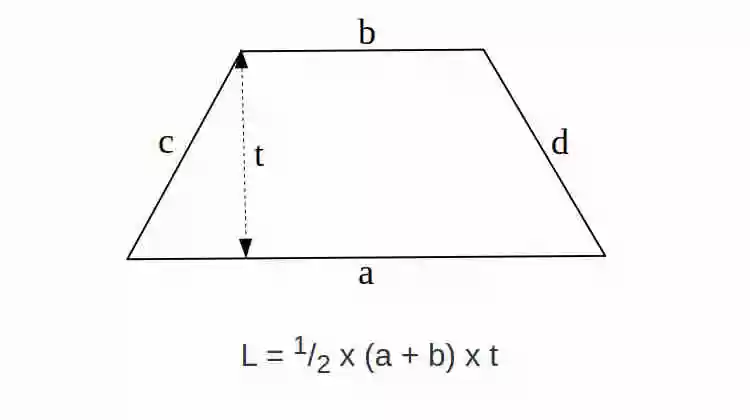
Rumus Luas Trapesium adalah L = 1/2 x (a + b) x t
Keterangan Variabel:
L = Luas
a = panjang sisi bawah
b = panjang sisi atas
t = tinggi
Contoh Soal: Suatu Trapesium memliki panjang a = 4 m (meter), b = 3 m (meter), dan tinggi = 2 m (meter), berapakah luas Trapesium?
Jawaban:
L = 1/2 x (a + b) x t
L = 1/2 x (4 m + 3 m) x 2 m
L = 1/2 x (7 m) x 2 m
L = 1/2 x 14 m
L = 14 m/2
L = 7 m2
Penggunaan
Keliling dan Luas Area suatu bangun datar berbentuk Trapesium memainkan peran penting dalam matematika modern. Selain kepentingannya yang jelas dalam geometri dan perhitungan, luas terkait dengan definisi determinan dalam aljabar linier, dan merupakan properti dasar permukaan suatu bidang dalam variabel geometri.
Rumus Matematika dasar dari suatu area atau bentuk datar 2 dimensi yang dibatasi oleh garis-garis lurus atau lengkung. Area bidang datar ini terdiri dari beberapa bentuk termasuk: persegi, segitiga, jajaran genjang, persegi panjang, trapesium, layang-layang, belah ketupat, dan lingkaran. Secara singkat, area datar tersebut memiliki nilai kuantitas keliling dan luas dalam satuan panjang dan satuan luas.